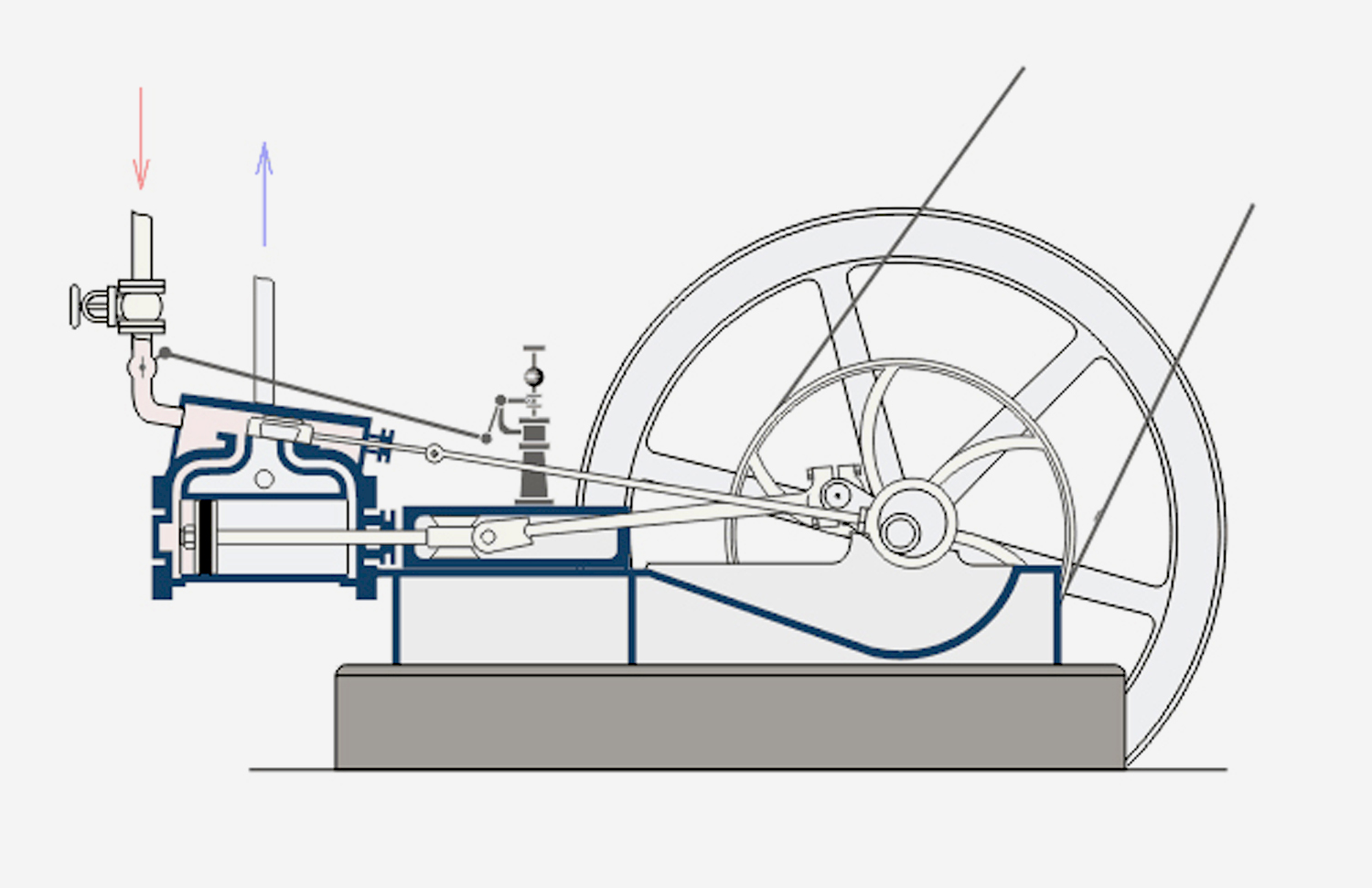
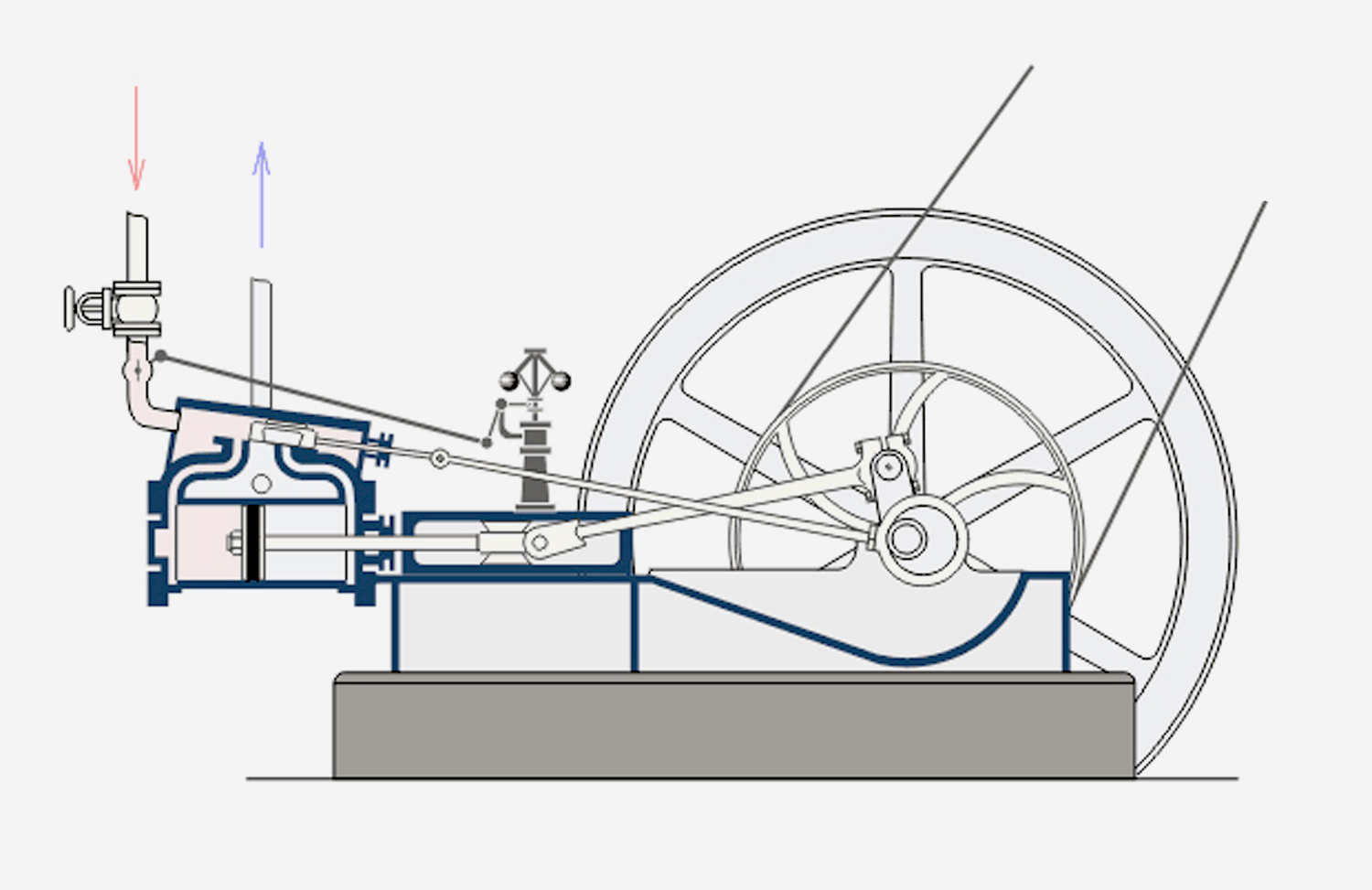
di Fabio Panfili
 L’idea di erigere un museo presso l’Istituto Tecnico Industriale G. e M. Montani risale a fine anni Ottanta.
L’idea di erigere un museo presso l’Istituto Tecnico Industriale G. e M. Montani risale a fine anni Ottanta.
Il Consiglio di Istituto di quel tempo, su sollecitazione di due persone lungimiranti(1), individuò come sede alcuni locali comunicanti e suggestivi a pianterreno (detti “le grotte”) dell’antico monastero degli Agostiniani, edificio divenuto proprietà del Montani nel 1903.
Poco dopo iniziarono i lavori di restauro dei locali. Però l’iniziativa non ebbe seguito per vari motivi, tra i quali le nuove leggi sulla sicurezza con l’esigenza di realizzare strutture antincendio ecc. , strutture che furono ubicate proprio nelle “grotte”.
L’Istituto Tecnico Industriale Montani di Fermo è forse il più antico d’Italia nel suo genere (1854 anno di fondazione). Seguono il Rossi di Vicenza e il Volta di Napoli.
È sorprendente la nascita di una scuola industriale in una provincia caratterizzata da una economia quasi esclusivamente agricola.
Ci si aspetterebbe dunque che una scuola così antica e così grande avesse un patrimonio di attrezzature tecnico scientifiche notevole. Purtroppo invece è mancata una cultura della conservazione, che non significa solo mettere gli oggetti sotto vetro, ma piuttosto recuperarne le funzioni nel loro contesto storico per trasmetterne il significato scientifico.
La perdita della gran parte degli strumenti elencati nei numerosi inventari si potrebbe attribuire alla carenza di luoghi di conservazione e alla necessità di far spazio a nuovi macchinari e strumentazioni nei laboratori, ma è una ipotesi debole per chi conosce bene le strutture dell’Istituto.
Ciò che resta appare comunque ricco e pregevole, ma la parte cospicua delle attrezzature e delle strumentazioni perdute avrebbe meglio rappresentato la storia industriale dell’intero Paese.
Come esempio di ciò che nel tempo è andato perduto al Montani, mi sembra significativo ricordare la scomparsa di un magnetron, acquistato nel 1941. Questo strumento nel 1938 era oggetto di studi serrati, in Inghilterra e al M.I.T. di Boston e ciò prova quanto questa Scuola si tenesse aggiornata. Il magnetron è il cuore del radar in fase di trasmissione e, per inciso, anche del comune forno a microonde.
 Un magnetron è in alto a sinistra nella foto di uno scorcio della Sala 4.
Un magnetron è in alto a sinistra nella foto di uno scorcio della Sala 4.
Riporto qualche dettaglio di tipo storico a supporto di quello che si è detto.
Nel primo inventario oggi esistente del 1906 sono elencati: officine di meccanica motrice e dinamo, fonderia, fabbri, falegnami, elettrotecnica; inoltre i gabinetti di meccanica, fisica e chimica, elettrotecnica, chimica e scuola di plastica.
Nei primi anni della sua fondazione, l’insegnamento pratico si articolava in molti indirizzi, ma la prima vera specializzazione fu la Meccanica. Furono istituite successivamente: l’Elettrotecnica (1903), la Chimica (1926), la Radiotecnica (1930), l’Elettronica Industriale (1959) e l’Informatica (1969), la denominazione di alcune di esse nel corso degli anni è stata modificata. Alcune sono scomparse sostituite da altre specializzazioni.

Alcuni strumenti di Chimica, scorcio della sala 4.
Molto esplicativa è una relazione scritta il 30 novembre 1935 dal Preside Mario Stella. All’epoca esistevano sei gabinetti scientifici, per un totale di tredici laboratori riguardanti: fisica, chimica, elettrotecnica, radiotecnica, tecnologia e macchine. I reparti di officina erano dieci: fonderia, falegnameria, torneria, montaggio, trattamenti termici, fucina, saldatura autogena, elettromeccanica, lavorazione del ferro.

Alcuni strumenti di Elettronica, scorcio della sala 4.
Il Montani e la sua storia si identificano con le sue officine, con i suoi laboratori, e con le numerosissime persone che vi hanno passato una parte della loro vita. In questa scuola c’è stato un continuo accumularsi di strumenti, cataloghi, schede di istruzioni, libri, inventari. Un felice intreccio che permette ricerche storiche, magari a volte frammentarie.
Un aspetto importante: questi strumenti non erano soltanto oggetti da vedere in dimostrazioni ex cathedra, ma venivano usati dagli studenti, erano quindi vissuti.
Essi dunque diventavano maestri silenti.

Si vuole qui sottolineare l’importanza di conservare la memoria dell’intreccio tra lo sviluppo delle idee e dell’uso degli strumenti e il fatto che, nel contempo, il loro studio può aprire nuovi orizzonti all’indagine e a nuove idee.
 La catalogazione degli strumenti dell’Istituto, non è scaturita da un preciso disegno, ma piuttosto da una serie di avvenimenti.
La catalogazione degli strumenti dell’Istituto, non è scaturita da un preciso disegno, ma piuttosto da una serie di avvenimenti.
Nel marzo del 1985 si tenne, nella Sala dei Ritratti del Palazzo dei Priori del Comune di Fermo, un convegno su “Temistocle Calzecchi Onesti e il coherer nella conquista della telegrafia senza fili”. L’ideatore del convegno era il prof. Mario Guidone.
Vi fu il coinvolgimento di vari Enti, di molte scuole superiori di Fermo e di vari scienziati dell’Università di Bologna.
Il gruppo di lavoro del Montani, di cui facevo parte, presentò una ricostruzione del primo apparecchio radio a onde a fascio di Marconi (1896). Questa fu una occasione per scovare nei laboratori del vasto ex convento, tuttora sede del Triennio, due potenti rocchetti di Ruhmkorff e un antico ricevitore telegrafico Morse, risalenti a fine Ottocento, e per restaurarli. Il restauro del ricevitore telegrafico Morse fu opera di Leone Bolognini, mentre Federico Balilli si occupò del rocchetto più grande e della costruzione di un coherer, con il supporto competente di Mario Guidone e del prof. Claudio Marcotulli.
Le antenne erano state messe a nostra disposizione dall’antico Liceo Classico A. Caro di Fermo, dove Calzecchi era stato allievo, aveva poi insegnato ed eseguito esperimenti sistematici sulle proprietà del tubetto a polveri metalliche negli anni 1894-85-86, esperimenti pubblicati su Il Nuovo Cimento.
Nel fuoco dell’antenna cilindrica a sezione parabolica del ricevitore marconiano, c’è infatti il coherer.
Questo fu un passo forse significativo.
Nel 1987 gli atti del convegno furono raccolti nella pubblicazione a cura di E. Fedeli e M. Guidone, La conquista della telegrafia senza fili, Temistocle Calzecchi Onesti e il coherer, Ed. Nuova Alfa Editoriale, Bologna, patrocinato dal Comune di Fermo e presentato in una conferenza.
 Nello stesso anno vennero messe nel corridoio che porta all’Aula Magna del Triennio del Montani le prime vetrine contenenti alcuni strumenti, senza un preciso progetto ma con il sogno di un futuro museo.
Nello stesso anno vennero messe nel corridoio che porta all’Aula Magna del Triennio del Montani le prime vetrine contenenti alcuni strumenti, senza un preciso progetto ma con il sogno di un futuro museo.
In questo periodo fu organizzata una mostra di esperimenti che ebbe una certa risonanza a livello regionale.

Nel luglio del 1990 il prof. Mario Guidone ed il prof. Ettore Fedeli inviarono al Consiglio di Istituto una bozza di delibera (1) per l’istituzione di un museo e, in seguito all’approvazione del Consiglio di Istituto(2 e 3), inviarono l’opportuna documentazione a Roma. I lavori nelle “grotte” iniziarono e se ne vede ancor oggi la sabbiatura delle antiche volte, ma il progetto non ebbe seguito, come si è già detto.
L’impulso più forte venne comunque dalla partecipazione della scuola alle Settimane della Cultura Scientifica dal 1993 al 1996. All’allestimento degli esperimenti da mostrare al pubblico contribuirono numerosi insegnanti e molti allievi, ma l’organizzazione si dovette a poche persone. Queste ultime sentirono la necessità di procedere lungo le direttive seguenti: 1°) la catalogazione e il restauro di antichi strumenti, 2°) il riordino dell’Archivio Storico e della Biblioteca.
Non ci furono fatti nuovi fino all’ottobre del 1998, la sezione di Fermo di Italia Nostra, sotto la presidenza del prof. Elvezio Serena, organizzò un convegno su “Il Montani di Fermo, tutela di un patrimonio”. A cui seguì nel novembre del 2000 la pubblicazione degli atti, per la salvaguardia del patrimonio dell’Istituto.
In seguito al sopralluogo effettuato dall’arch. D. Cardamone, su sollecitazione del Presidente del Consiglio di Istituto Luciano Scafà, nel maggio del 2000, la Soprintendenza per i Beni Ambientali e Architettonici della Regione Marche richiese una documentazione, che comprendeva tra l’altro una precisa catalogazione degli strumenti più significativi, aventi oltre cinquanta anni, per essere sottoposti a tutela, secondo quanto previsto dall’art. 3 del Testo Unico n°440 del 1999. (4)

Alcuni strumenti di Meccanica, scorcio della Sala 4.
Un grosso problema della catalogazione riguarda i numerosi inventari che vanno dal 1906 ad oggi, e ognuno di essi è il risultato di un censimento fatto con numerazioni e sigle diverse dagli altri. Ciò comporta che sullo strumento si trovano numeri e sigle di varia e incerta provenienza. Inoltre lo stesso apparecchio viene, negli anni, descritto con nomi diversi e a volte errati: nel 1906 il metro campione viene chiamato “Pisati”, nel 1912 si chiama “metro campione in cassetta” e tale rimarrà fino al 1956. Nessuno può oggi garantire che sia lo stesso! Ma Giuseppe Pisati non era un costruttore, anzi era uno scienziato che si occupava di metrologia, e per un certo periodo insegnò in Ancona. Una ipotesi con qualche fondamento è che detto metro sia della Max Kohl e che forse un professore del Montani abbia chiesto a Pisati un consiglio su quale metro acquistare. Però è anche strano che l’oggetto non riporti il marchio della Max Kohl.
A volte l’identificazione degli strumenti è molto difficoltosa: l’elettroscopio di Wulf, ad esempio, era stato classificato come strumento ottico, perché attraverso una lente si osservava un tubo vuoto. Del resto si ignorava l’esistenza di questo tipo di elettroscopio, fino a quando io, consultando sistematicamente vecchie schede di istruzioni della casa costruttrice Leybold, lo identificai.
Nelle istruzioni c’era inoltre il disegno dell’equipaggio mobile e questo fu rinvenuto dal tecnico di laboratorio Federico Balilli, che ha una prodigiosa memoria degli strumenti in dotazione del laboratorio di fisica e li sa restaurare.
Oggi l’elettroscopio, datato 1941, fa bella mostra di sé al MITI e si può osservare il fermaglio di quarzo, sottile come il filo di una tela di ragno, che tende la fogliolina di alluminio dell’equipaggio mobile all’interno del tubo.

Il metro campione è in basso a sinistra nella foto di uno scorcio della Sala 4; l’elettroscopio di Wulf è in alto a destra.
Riprendo il filo storico del discorso.
Nel 2004 venne il grande progetto della Mostra Scientifica per il 150° anniversario della nascita della Scuola. La realizzazione della mostra fu affidata dal Comune di Fermo (uno degli enti promotori) a dei bravi professionisti. Parteciparono vari enti e associazioni, comprese la Provincia di Ascoli Piceno e la Cassa di Risparmio di Fermo. Un Comitato doveva scegliere gli ambienti e soprattutto pochi e significativi apparecchi.
 Alcuni strumenti di Radiotecnica, scorcio della sala 4.
Alcuni strumenti di Radiotecnica, scorcio della sala 4.
Il vicepreside prof. Mauro Tomassetti si distinse per le sue capacità organizzative.
La mostra ebbe una forte risonanza e grande partecipazione, anche per l’attaccamento di numerosissimi ex alunni alla Scuola.
Questo avvenimento fu forse il più decisivo per lo sviluppo dell’idea di realizzare un museo.
Ne seguì la pubblicazione di un bel volume, I.T.I. ‘MONTANI’ FERMO 150 Scuola Tecnica Società Moderna, edito da Nardini Firenze.
 Alcuni strumenti di Elettrotecnica, scorcio della sala 4.
Alcuni strumenti di Elettrotecnica, scorcio della sala 4.
Nel 2005, su idea della dirigente prof.ssa Silvia Fazzini e con il supporto di numerosi sponsor, furono pubblicati due libri in unico cofanetto: IL MONTANI Storia dell’Istituti Tecnico Industriale di Fermo, di Settimio Virgili e STRUMENTI NELLA STORIA DEL MONTANI di Fabio Panfili(5).

Alcuni dispositivi di Informatica, scorcio della sala 4.
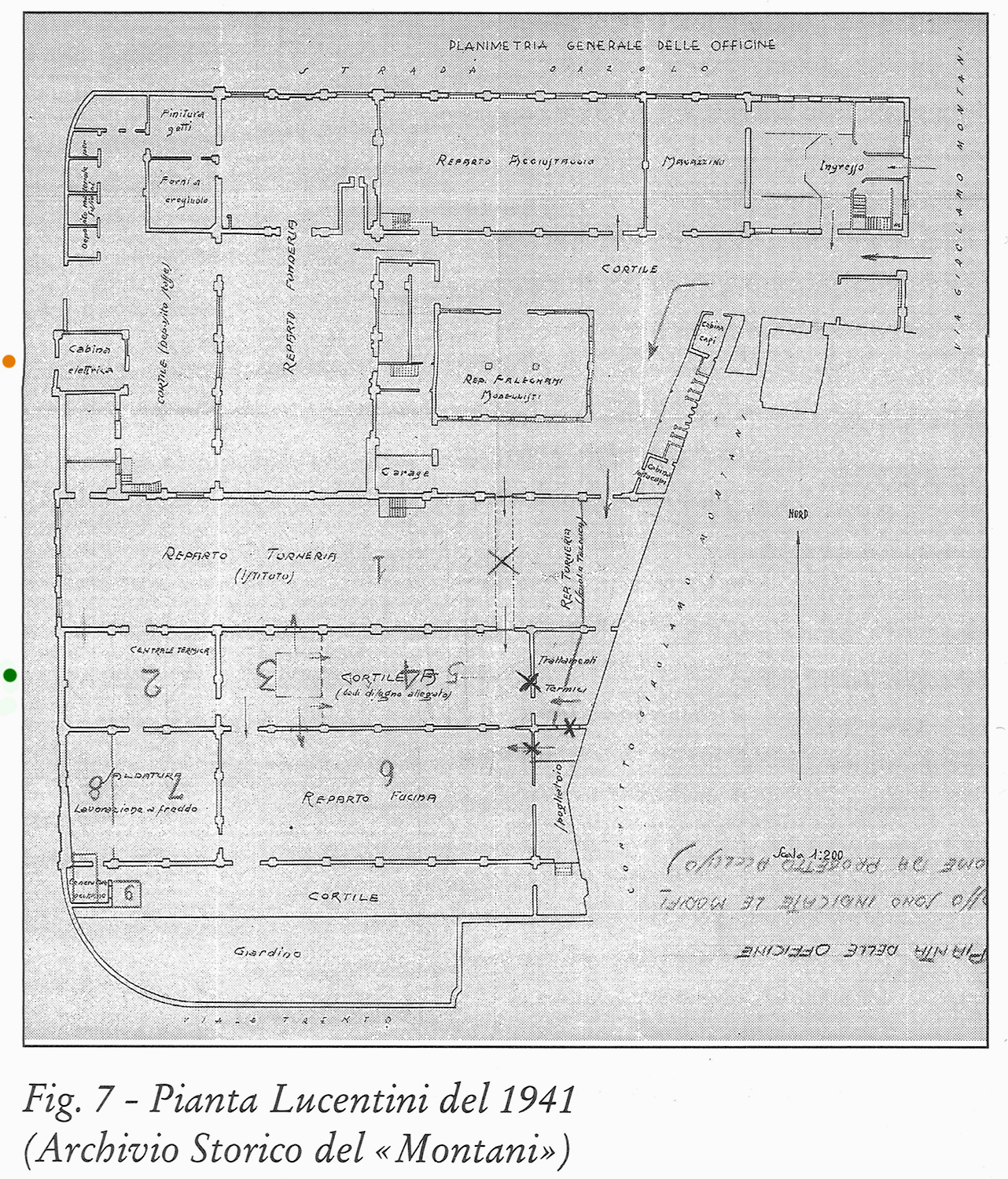
In questo periodo, la Provincia di Ascoli Piceno, presidente Massimo Rossi, fece redigere i progetti dettagliati sulla fattibilità del museo; le antiche officine meccaniche, esempio notevole di archeologia industriale, diventarono la sua sede naturale.

L’Assessorato alla Cultura di Ascoli Piceno, per il fattivo e costante interessamento soprattutto della titolare prof.ssa Olimpia Gobbi, era riuscito a destinare una cifra ragguardevole per l’istituzione del Museo del Montani.
Nel frattempo Olimpia Gobbi aveva chiesto ai dirigenti del Museo della Scienza e della Tecnologia “Leonardo da Vinci” di Milano (dott. Salvatore Sutera ed altri) di indicarle a chi rivolgersi per la progettazione del museo, inoltre si mise in contatto con i dirigenti del Museo del Balì.
In estate un gruppo di responsabili del Museo di Milano, su invito sempre di Olimpia Gobbi, visitò il Montani.
Fu così scelta la Società Sissa Medialab di Trieste, esperta nella divulgazione a carattere scientifico, per il progetto, gli allestimenti, per una attenta ricognizione degli spazi, degli strumenti e dei documenti, e per le dimostrazioni didattiche rivolte al pubblico.
Ricordo in particolare la prof.ssa Paola Rodari (nel 2021 ne è la Presidente) che coordinava l’equipe, per le sue profonde conoscenze nel campo della comunicazione pubblica della scienza e in particolare nella progettazione e realizzazione di mostre e musei della scienza e della tecnologia.
La Rodari conserva piacevoli ricordi della permanenza a Fermo, per l’entusiasmo e la passione con cui svolse l’incarico nei luoghi ricchi di storia e suggestivi come il Triennio e le Antiche Officine.
Il progetto fu affidato all’architetto Giovanni Panizon che ha una vastissima esperienza nel campo, come si può vedere nel sito:
https://www.giovanniandreapanizon.it/ .
In particolare si veda il link:
https://www.giovanniandreapanizon.it/project/m-i-t-i-museo-della-innovazione-e-della-tecnologia-industriale-a-fermo/
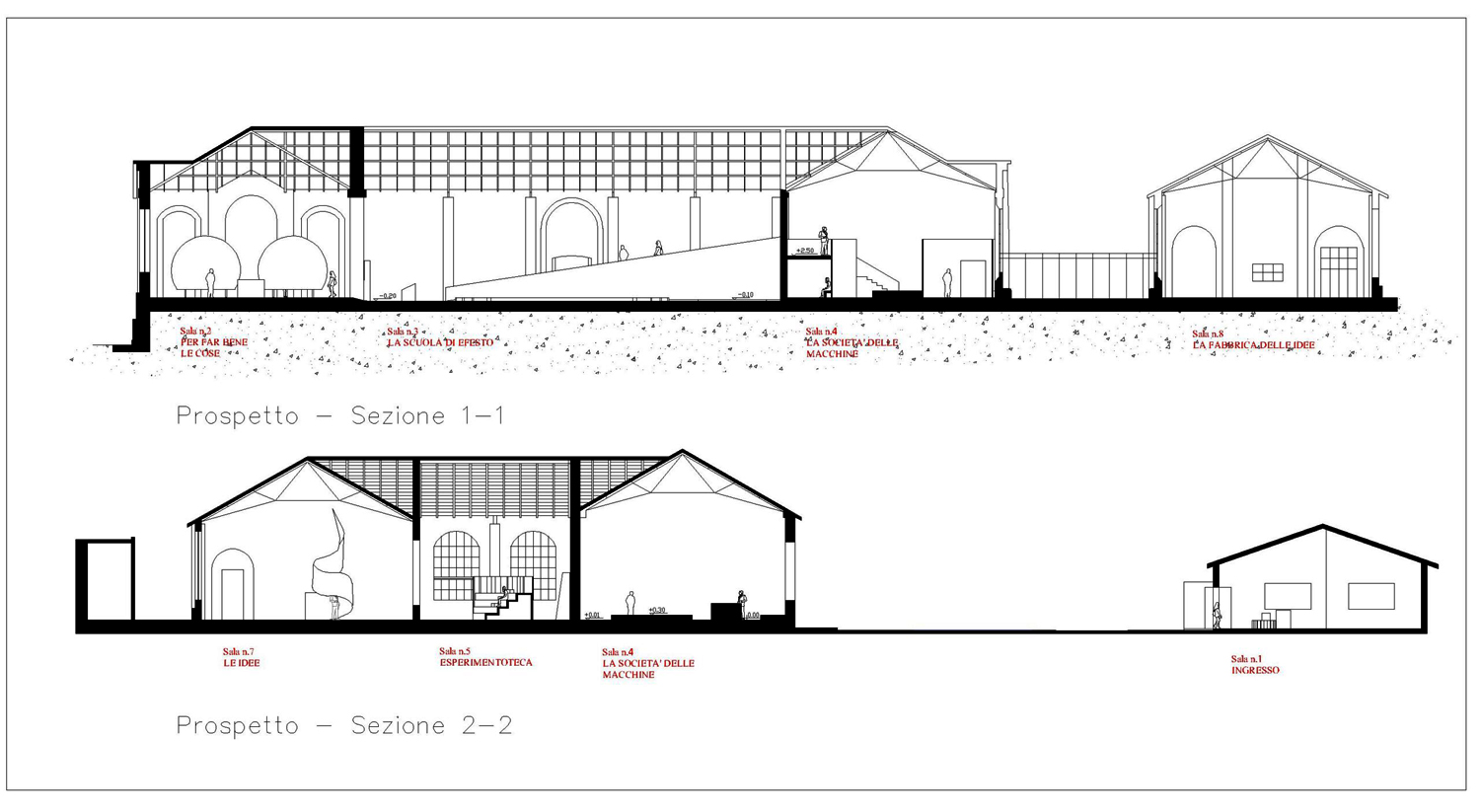
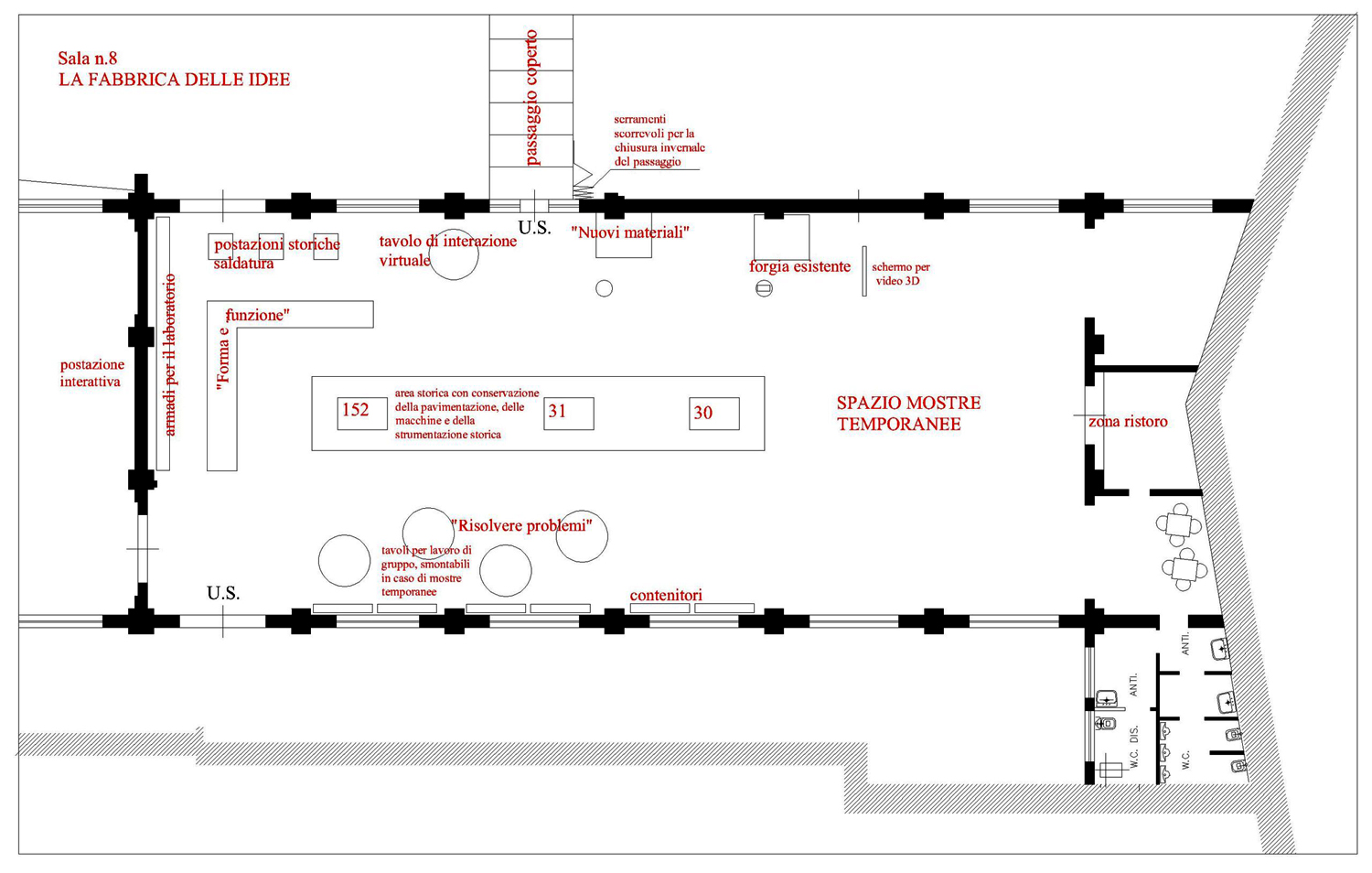
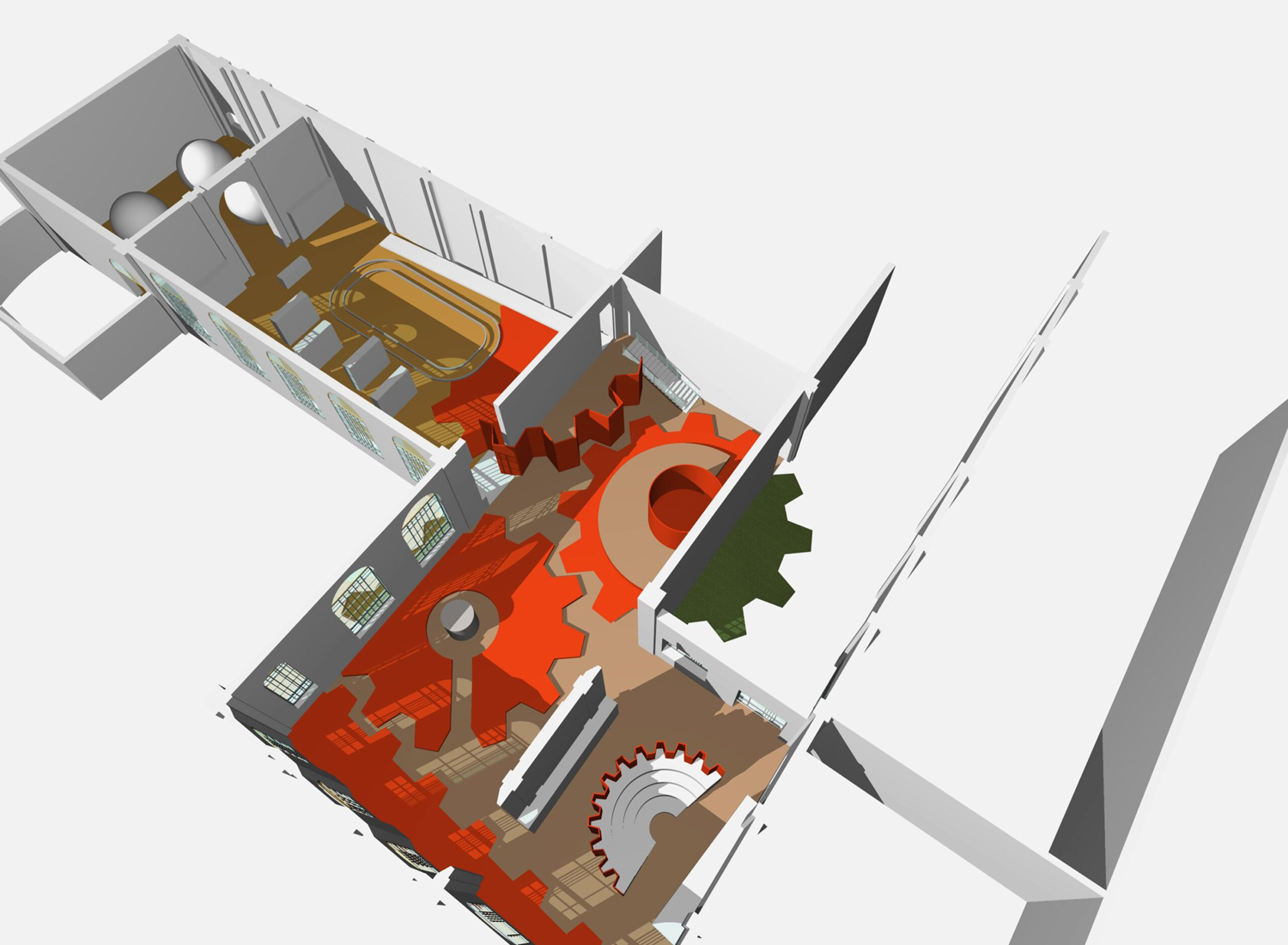
I disegni qui riportati sono parte del progetto e sono pubblicati col permesso sia della prof.ssa Paola Rodari, sia dell’arch. Giovanni Panizon.
Il gruppo di Trieste soggiornò a lungo a Fermo per studiare attentamente gli aspetti dei luoghi e la loro storia.
Paola Rodari ha anche coniato il nome M.I.T.I., per il Museo, legando un acronimo con il nomignolo ITI dato usualmente al Montani: Museo dell’Innovazione e della Tecnica Industriale.
 Ho riportato una foto nella quale si vede bene che il nomignolo ITI ha ispirato i progettisti del Biennio, aperto nell’anno scolastico 1963/64.
Ho riportato una foto nella quale si vede bene che il nomignolo ITI ha ispirato i progettisti del Biennio, aperto nell’anno scolastico 1963/64.
Nel novembre del 2005 fui invitato dal Direttore Generale Fiorenzo Galli, su segnalazione del Dirigente dott. Salvatore Sutera, al Museo Nazionale della Scienza e della Tecnologia “Leonardo da Vinci” di Milano per partecipare ad uno Workshop “La catalogazione del patrimonio scientifico e tecnologico”.
Per gli “esempi di valorizzazione di collezioni di istituti scolastici” c’eravamo: Loredana Mattalia del Liceo “A. Volta” di Como; Marco Zulian, Collegio San Francesco P. B. di Lodi; ed io che dovevo illustrare il patrimonio tecnico scientifico del Montani e poi collaborare ad alcune loro iniziative didattiche.
Allo workshop intervennero, oltre a Salvatore Sutera, Laura Ronzon e Vincenzo Iannone, membri del Museo organizzatore, i seguenti esperti:
Flavia Ferrante dell’Istituto Centrale per il Catalogo (ICCD), Roma.
Paolo Brenni, CNR.
Pasquale Tucci, Istituto di Fisica Generale e Applicata, Università degli Studi di Milano.
Paolo Castellani, ICCD.
Mara Miniati e Iolanda Roffo, Istituto e Museo di Storia della Scienza, Firenze.
Enzo Minervini, Sistema Informativo Regionale Beni Culturali (SIRBEC), Regione Lombardia.
Restai sorpreso dalla affabilità di esperti di tale livello, che furono ben lieti nel darmi, negli anni che seguirono, consigli e informazioni.
Salvatore Sutera mi inviò una lettera che conservo tuttora.
Paolo Brenni mi regalò bellissimi cataloghi di strumenti di cui è l’autore, e i seguito mi diede preziosi consigli su alcuni strumenti della collezione del Montani, riportati nel sito.
Pasquale Tucci, come gli altri, restò in contatto con me via e.mail.
Mara Miniati venne addirittura a Fermo, su mio invito e in via ufficiale dell’Istituto, per partecipare ad una Giornata della Scienza – Premio “Mario Guidone” presso il Montani; il suo intervento incantò il pubblico.
Nel 2008-2009 la Facoltà dei Beni Culturali, Corso di Laurea Magistrale, dell’Università di Macerata, con sede a Fermo, su indicazione del prof. ing. Giuseppe Calcinaro, mi chiamò per tenere un breve corso sul “Laboratorio di valorizzazione del patrimonio scientifico e tecnico delle Marche”.
Ho ricordato tutto ciò per documentare il risveglio tangibile dell’attenzione verso la valorizzazione degli strumenti antichi avvenuto in quegli anni.
Nel 2009 divenne operativa la Provincia di Fermo che si assunse il compito di costruire il Museo MITI attuale e questi avvenimenti sono, tutto sommato, recenti.
Il MITI è stato inaugurato il 22 dicembre del 2012.
Chi desidera informazioni al riguardo può andare al link “Museo MITI”, che si trova nel sito dell’ITT G. e M. Montani nell’elenco a destra; può inoltre visitare il link
http://www.breschistudio.com/project/allestimento-museo-dellarcheologia-industriale/.
del sito Breschi Studio.
Il mio ringraziamento va a Settimio Virgili, per la gentile collaborazione ed i preziosi suggerimenti nella stesura di questo articolo.
Ringrazio Paola Rodari, Giovanni Panizon e Olimpia Gobbi.
Le foto del MITI sono di Claudio Profumieri che ringrazio.
Per ingrandire le immagini cliccare su di esse col tasto destro del mouse e scegliere tra le opzioni.
Appendice documentaria e note
(1) Riporto qui ampi stralci della bozza di delibera scritta da Ettore Fedeli e Mario Guidone.
Signori Consiglieri,
l’idea di istituire un museo per documentare il ruolo svolto dal Montani, istituto primogenito in Italia, è stata più volte avanzata e dibattuta dal nostro Consiglio di Istituto.
Oggi sembrano essere maturate le condizioni per realizzare questa generosa e legittima aspirazione della nostra Scuola e dell’intera comunità cittadina.
La consapevolezza della enorme importanza storica e culturale del patrimonio tecnico-scientifico d’Italia comincia, infatti, a produrre iniziative concrete per la sua tutela e valorizzazione.
Con la C. M. del 12 gennaio 1989, avente per oggetto la “Ricognizione del materiale archivistico di rilevanza storico-scientifica esistente presso Istituti Tecnici, Licei Scientifici ed Istituti Magistrali”, il Ministero della Pubblica Istruzione ha avviato nelle scuole una prima fase di censimento del patrimonio esistente, in vista della predisposizione di un progetto globale avente come fine ultimo “non soltanto una migliore conservazione materiale, pur indispensabile, della documentazione, ma il suo recupero per sempre più diffuse esigenze di ricerca, e quindi la sua fruibilità”.
Successivamente il Ministero per l’Università e la Ricerca Scientifica e Tecnologica ha predisposto un Progetto Finalizzato, presentato dal prof. Giorgio Dragoni al Convegno tenuto a Pavia dall’11 al 15 settembre 1989, al quale hanno partecipato i proff. Mario Guidone ed Ettore Fedeli in qualità di membri del GNSF (Gruppo Nazionale di Storia della Fisica) del CNR-Unità di Bologna.
Il prof. Dragoni, presidente del GNSF del CNR, membro del Comitato per la Tutela e la Diffusione della Cultura Scientifica e Storico-Scientifica insediato all’uopo dal Ministro Ruberti, si è detto disponibile per una ricognizione del materiale tecnico-scientifico della nostra scuola, una volta attivate le prime operazioni di catalogazione e restauro conservativo e funzionale. Una prima realizzazione del progetto si è mostrata nel Convegno tenuto a Bologna il 10-11 marzo 1990 sul tema “Una realtà straordinaria. Il Patrimonio Storico Scientifico Italiano”.
In quel Convegno studiosi e ricercatori provenienti dalle principali Università italiane hanno riferito su studi, ricerche, censimenti, catalogazione, informatizzazione del patrimonio esistente.
La prossima iniziativa promossa dal Comitato per la Tutela e la Diffusione della Cultura Scientifica e Storico-Scientifica del MURST sarà denominata SETTIMANA DEI MUSEI SCIENTIFICI e si svolgerà dal 10 al 15 dicembre 1990 a Roma e, simultaneamente, nelle sedi locali in grado di attivare manifestazioni complementari (Milano: Brera, Pavia, Firenze, Bologna, Napoli, etc.) .
Si tratta di una grande iniziativa di carattere nazionale e di forte richiamo anche a livello internazionale, con iniziative locali in tutte le Sedi che siano in grado di attivare manifestazioni specifiche. Essa ha lo scopo di focalizzare l’opinione pubblica sulle problematiche del patrimonio storico scientifico e di favorire il reperimento di fondi presso Enti e Ditte pubbliche e private, oltre a quelli già stanziati dai competenti ministeri.
Il “Montani” con la sua tradizione, il suo patrimonio tecnico-scientifico e le sue potenzialità operative possiede tutti i requisiti per partecipare, attraverso il locale gruppo GNSF del CNR con pieno diritto all’iniziativa, sia inviando materiali significativi alla Mostra Nazionale documentando la sua primogenitura, sia, soprattutto, dando il via alla istituzione di un proprio Museo Tecnico-Scientifico.
Tale Museo garantirebbe non solo la conservazione di un inestimabile patrimonio di strumenti, ma una nuova irradiazione di quella cultura politecnica che è già pervenuta, nel passato, a industrie italiane e straniere.
(2) Verbale n° 211 del 05/07/1990
Approvazione istituzione di un museo tecnico scientifico nella Scuola. Il Presidente (Iobbi Mariano) legge la bozza di delibera approntata; si propone di ubicare i locali nei sotterranei della scuola. La problematica viene illustrata dal prof. Fedeli che mette in risalto le possibilità che si aprono e gli eventuali benefici della proposta (gite d’istruzione, materiali reperibili, facilità di approntamento del materiale). Calcinaro esprime perplessità in merito ai tempi di realizzazione, una volta assunta la delibera nella quale la prima scadenza è fissata al 15/12/1990. Propone un comitato “ad hoc” composto dai rappresentanti delle amministrazioni locali e del “Montani”. Luciani: dare disponibilità dei locali e dei materiali ed acquisire il deliberato dell’Ente Locale. Esce il cons. Cordella. Pucci Sisti: “operare senza porsi eccessivi problemi”. Panfili: utilizzare i locali della scuola e nel contempo iniziare il lavoro di sistemazione con il relativo progetto. Viene proposto il Comitato: Serdoz, Aragusta, Maranesi, Preside, Raccichini, Concetti, Fedeli, Guidone, Presidente del Consiglio, Luciani e quanti altri si rendessero disponibili. Approvato all’unanimità.
A questo farà seguito la seduta consiliare del 23/08/1990, in cui, in seguito alla partecipazione di Mario Guidone ed Ettore Fedeli, in qualità di membri del Gruppo locale del GNSF (gruppo nazionale di storia della fisica) del CNR, ad un convegno tenuto a Pavia sul Progetto Finalizzato, si delibera di inviare parte degli strumenti alla Mostra Nazionale che si terrà in dicembre (1990) a Roma.
(3) Estratto del Verbale del 23/08/1990 pag. 108-109
Ipotesi di ricognizione del materiale tecnico scientifico della Scuola, effettuabile dal prof. Dragoni presidente del GNSF del CNR, membro del Comitato per la Tutela e la Diffusione della Cultura Scientifica e Storico-Scientifica, nominato dal ministro Ruberti.
Mario Guidone ed Ettore Fedeli (in qualità di membri del GNSF) partecipano al Convegno tenuto a Pavia in cui il Ministero dell’Università e della Ricerca (M.U.R.S.T.) ha predisposto un progetto finalizzato.
Il Montani invia parte degli strumenti alla Mostra Nazionale, dando il via all’Istituzione del proprio Museo.
(4) Riporto qui l’elenco inerente all’invito all’Istituto a trasmettere la documentazione degli atti di tutela:
– Elenco generale degli strumenti e delle attrezzature; – Relazione sulle singole apparecchiature sotto il profilo Storico, Tecnico e Scientifico;- Documentazione fotografica; Planimetria catastale dei laboratori, delle officine e Dell’Istituto Montani;- Estratto di mappa comprendente il mappale relativo all’edificio quelli ad esso circostanti per un raggio di almeno m. 100 con chiaramente indicati i numeri di mappa;- Certificazione catastale relativa alle Ditte proprietarie dell’immobile di cui trattasi con relativa residenza e codice fiscale o partita I.V.A.;- Esauriente documentazione fotografica (n. 2 copie) sia degli interni che degli esterni dell’immobile;-Relazione storico-artistica ed eventuale materiale bibliografico o d’archivio sull’edificio.
[N.d.R.: chi ha redatto l’invito probabilmente ignora cosa comporta soddisfare la seconda richiesta: ogni strumento antico richiede settimane di ricerche solo per una corretta descrizione storico-scientifica].
(5) La seconda edizione, su iniziativa della Dirigente Prof.ssa Margherita Bonanni, è stata data in stampa nel 2018.
 Il Tombolone scientifico è un insieme di giochi scientifici costituiti da 90 esperimenti interattivi organizzati nei vari plessi dell’Istituto. I partecipanti ricevono una cartella con 5 numeri corrispondenti a 5 esperimenti e, sotto la guida di uno staff di studenti e docenti del Montani, ognuno di essi arriverà a fare “Tombolone” svolgendo e/o assistendo alle esperienze assegnate; tutti riceveranno un premio inerente alla curiosità scientifica e tecnica.
Il Tombolone scientifico è un insieme di giochi scientifici costituiti da 90 esperimenti interattivi organizzati nei vari plessi dell’Istituto. I partecipanti ricevono una cartella con 5 numeri corrispondenti a 5 esperimenti e, sotto la guida di uno staff di studenti e docenti del Montani, ognuno di essi arriverà a fare “Tombolone” svolgendo e/o assistendo alle esperienze assegnate; tutti riceveranno un premio inerente alla curiosità scientifica e tecnica.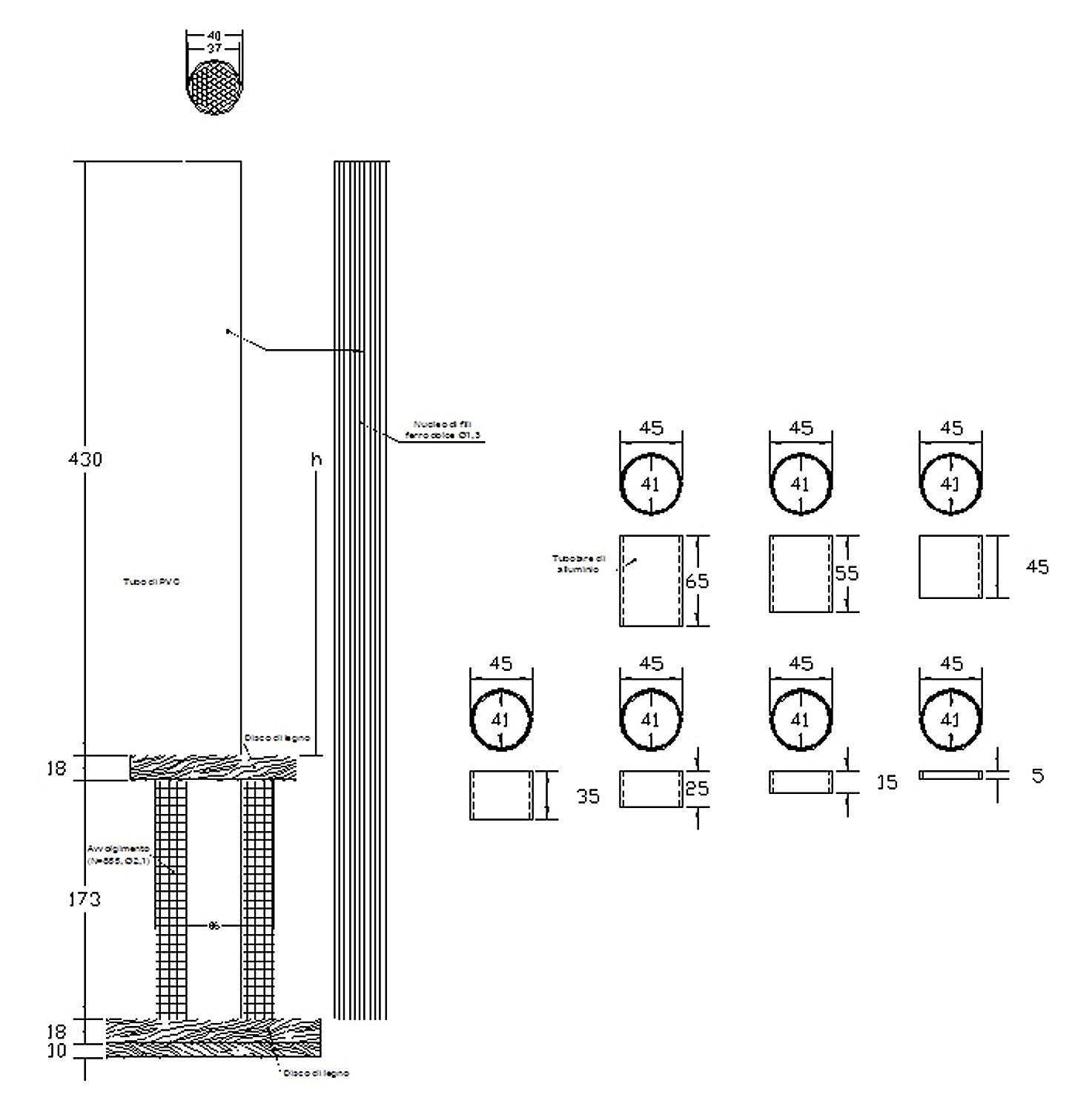

 Le numerose misure condotte in laboratorio hanno consentito di determinare tutti i parametri elettrici del modello circuitale della bobina.
Le numerose misure condotte in laboratorio hanno consentito di determinare tutti i parametri elettrici del modello circuitale della bobina.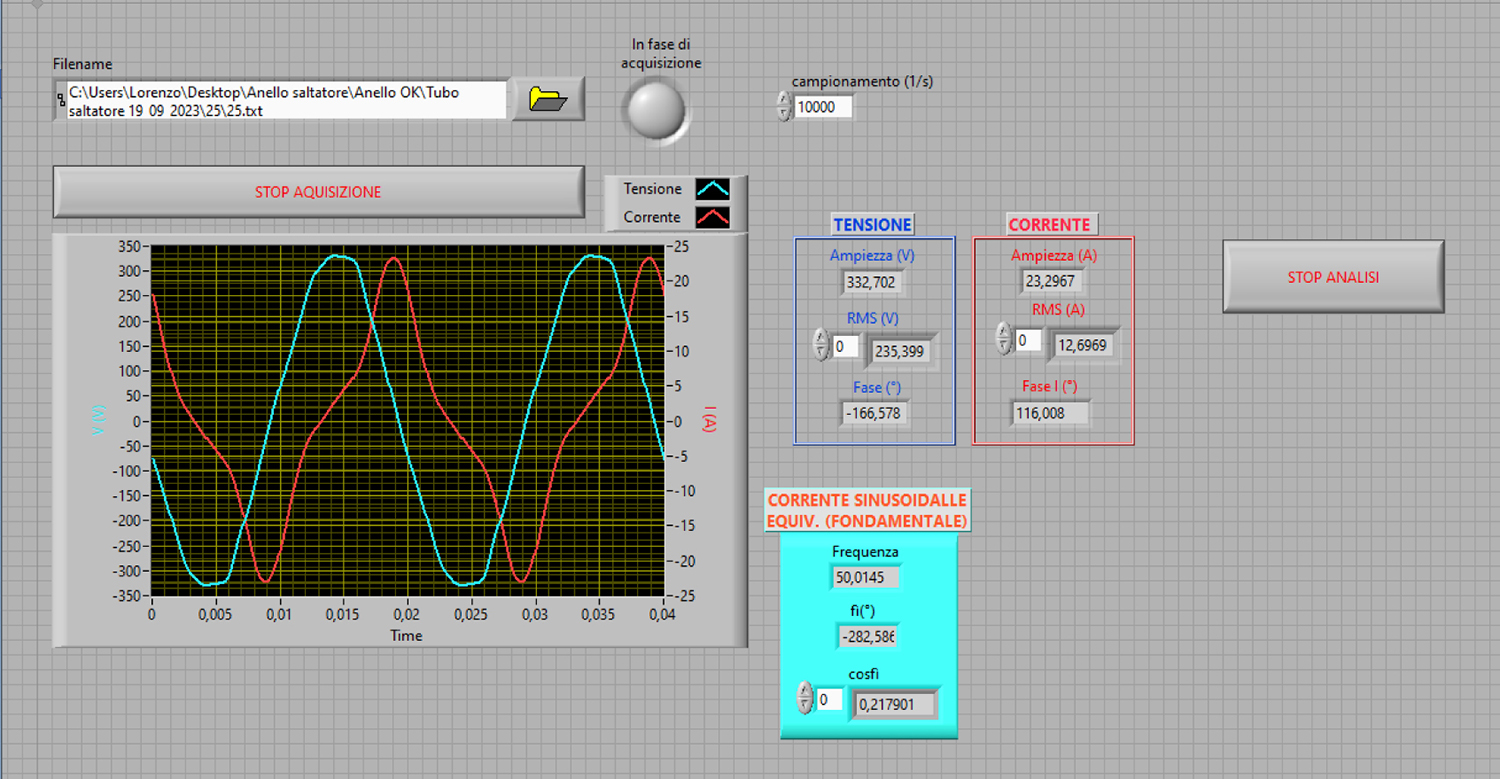 Figura 2 – Schermata elaborazione dati acquisiti con MeetBOX.
Figura 2 – Schermata elaborazione dati acquisiti con MeetBOX. Figura 3 – Andamento delle correnti nella bobina (I1) e nel cilindretto cavo (I2).
Figura 3 – Andamento delle correnti nella bobina (I1) e nel cilindretto cavo (I2).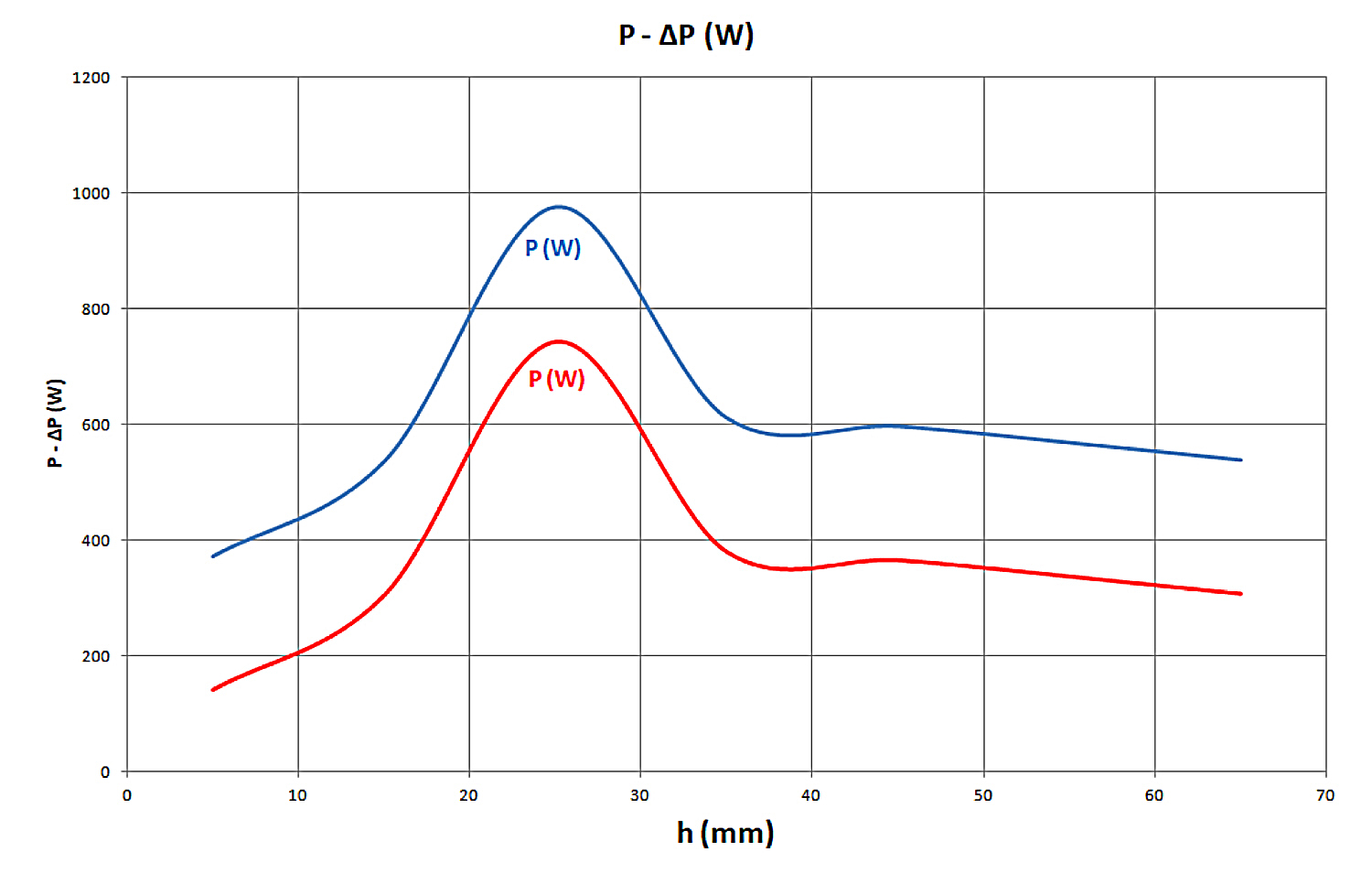 Figura 4 – Potenza assorbita dalla bobina e potenza dissipata nel cilindretto cavo.
Figura 4 – Potenza assorbita dalla bobina e potenza dissipata nel cilindretto cavo.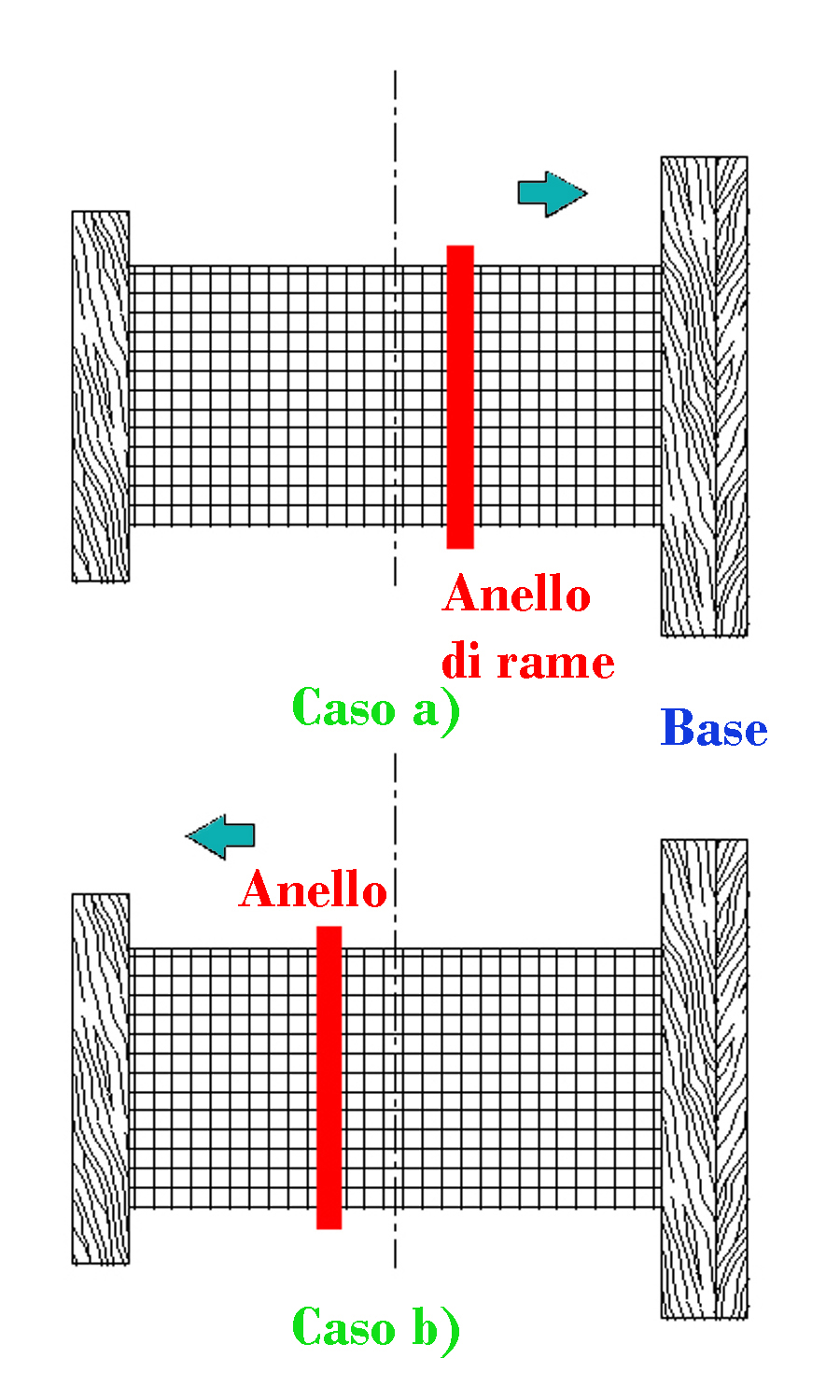 Figura 5 – Un esperimento inusuale
Figura 5 – Un esperimento inusuale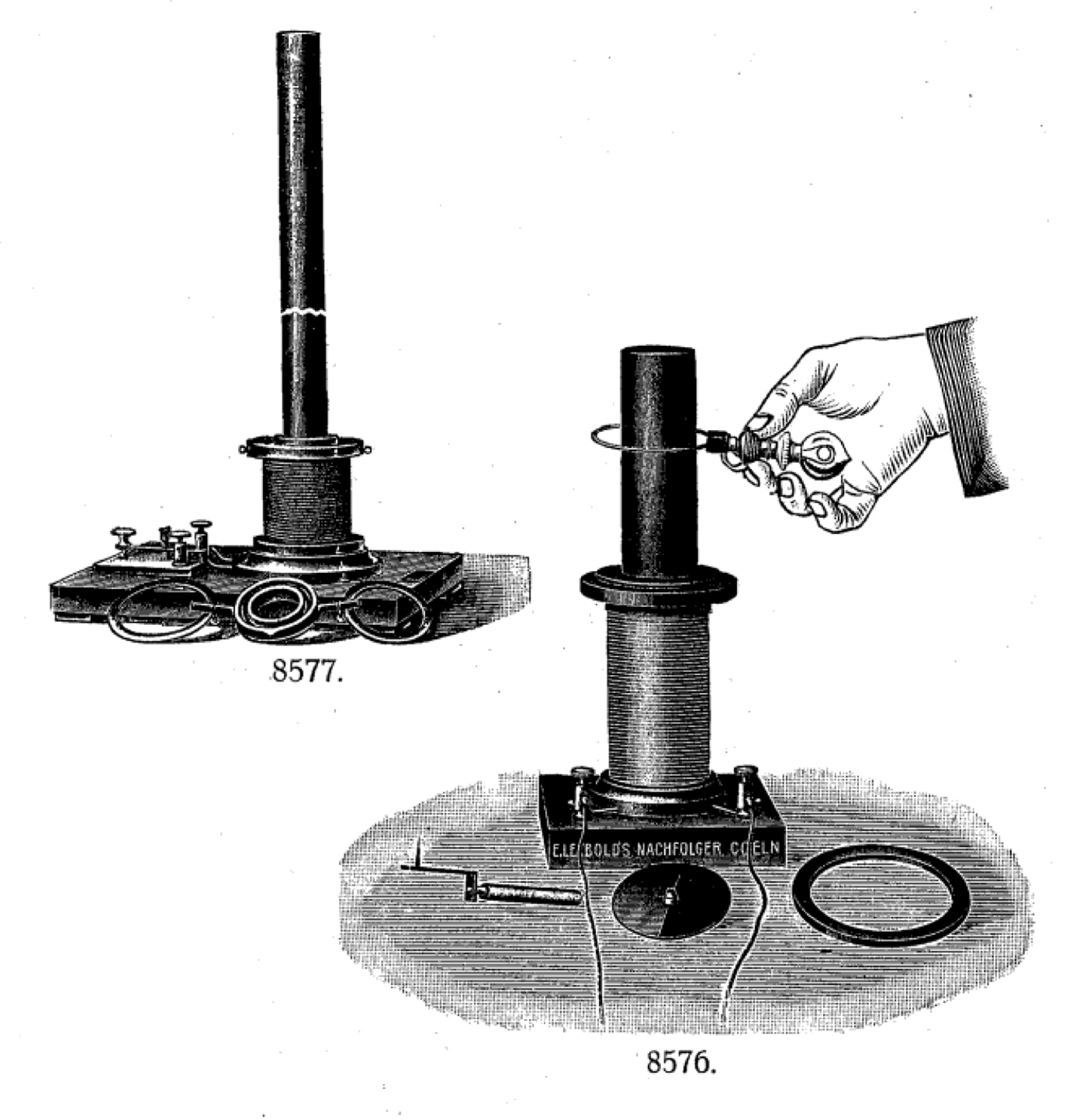 Nelle due figure tratte da Catalogue des Appareils pour l’Enseignement de la Physique construits par E. Leybold’s Nachfolger Cologne, 1905; rinvenibile all’indirizzo:
Nelle due figure tratte da Catalogue des Appareils pour l’Enseignement de la Physique construits par E. Leybold’s Nachfolger Cologne, 1905; rinvenibile all’indirizzo:

 Figura 7 – Il cannone elettromagnetico. Il disco è fotografato spostato per mettere in evidenza la bobina. Il condensatore è il grosso cilindro nero sulla destra, mentre il teleruttore e in primo piano.
Figura 7 – Il cannone elettromagnetico. Il disco è fotografato spostato per mettere in evidenza la bobina. Il condensatore è il grosso cilindro nero sulla destra, mentre il teleruttore e in primo piano.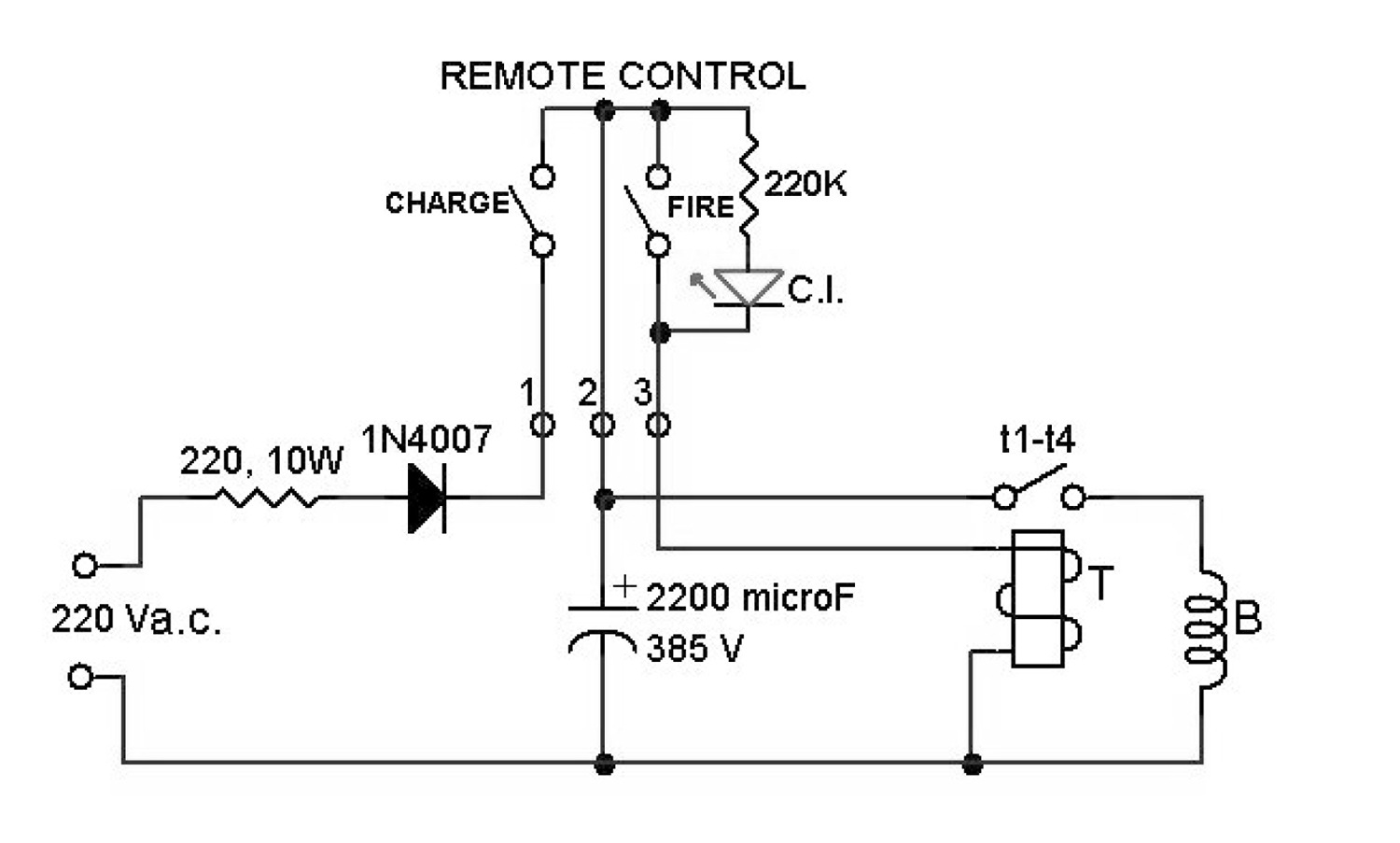 Figura 8 – Schema del Cannone Elettromagnetico. T è un teleruttore con i quattro contatti t1 – t4 in parallelo. C.I. è un diodo LED che indica il livello di carica del condensatore. REMOTE CONTROL è il telecomando, opportuno per motivi di sicurezza.
Figura 8 – Schema del Cannone Elettromagnetico. T è un teleruttore con i quattro contatti t1 – t4 in parallelo. C.I. è un diodo LED che indica il livello di carica del condensatore. REMOTE CONTROL è il telecomando, opportuno per motivi di sicurezza.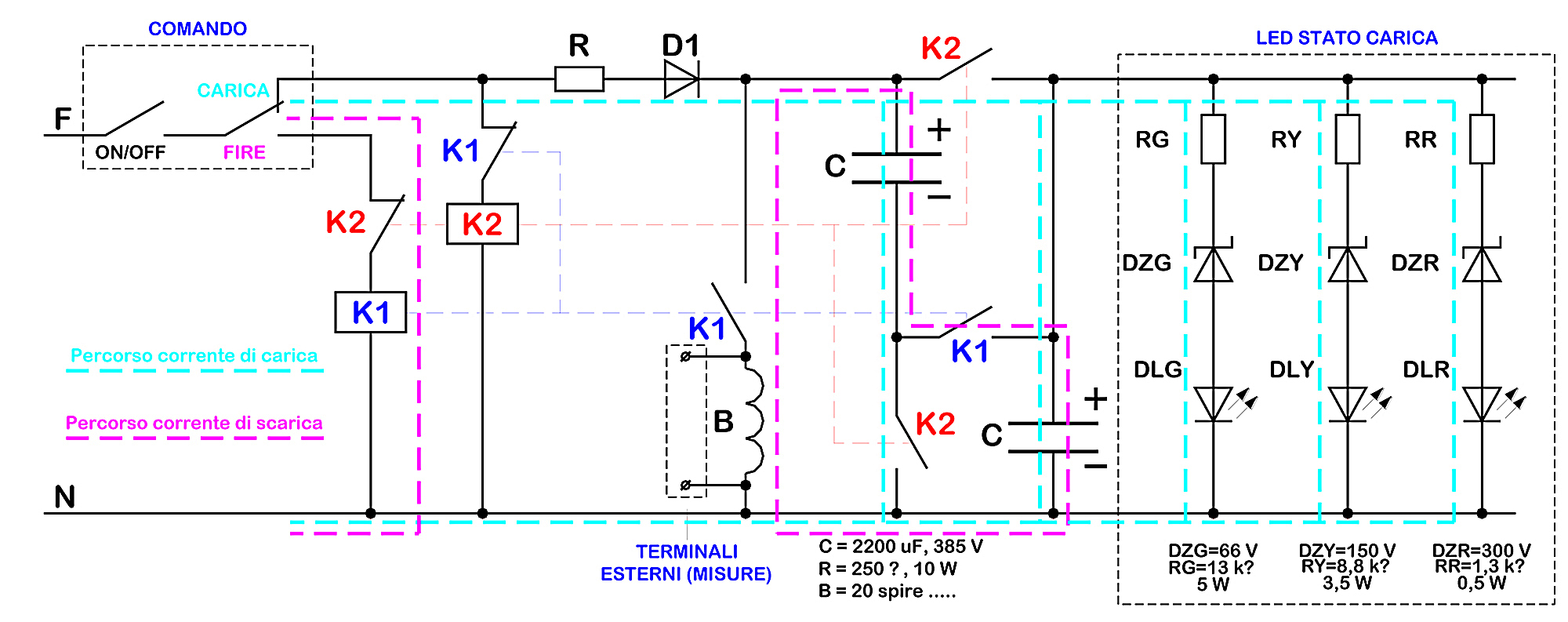 Figura 6 – Schema circuitale della variante del “cannone elettromagnetico”.
Figura 6 – Schema circuitale della variante del “cannone elettromagnetico”.